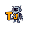가우시안 RBF 커널에 대해 알아보겠습니다. 오늘은 기계학습에서 중요한 역할을 하는 가우시안 RBF 커널에 대해 자세히 설명드리겠습니다. 이 커널은 데이터의 비선형성을 처리하는 데 매우 유용하며, 다양한 머신러닝 알고리즘에서 널리 사용됩니다.
가우시안 RBF 커널은 Radial Basis Function의 일종으로, 주로 서포트 벡터 머신(SVM)에서 사용됩니다. 이 커널은 두 점 사이의 거리를 기반으로 하여, 데이터 포인트 간의 유사성을 측정합니다. 즉, 두 점이 가까울수록 커널 값이 높아지고, 멀어질수록 커널 값이 낮아지는 특징을 가지고 있습니다.
가우시안 RBF 커널의 수학적 표현
가우시안 RBF 커널의 수학적 표현은 다음과 같습니다:
[ K(x_i, x_j) = \exp\left(-\gamma |x_i - x_j|^2\right) ]
여기서 ( K )는 커널 함수, ( x_i )와 ( x_j )는 두 입력 벡터, ( \gamma )는 커널의 폭을 조절하는 하이퍼파라미터입니다. 이 식은 두 점 간의 유클리드 거리의 제곱을 기반으로 하여, 거리가 멀어질수록 커널 값이 급격히 감소하는 형태를 가집니다.

가우시안 RBF 커널의 특징
가우시안 RBF 커널의 주요 특징은 다음과 같습니다:
- 비선형성 처리 : 데이터가 비선형적으로 분포되어 있을 때, RBF 커널은 효과적으로 이를 처리할 수 있습니다.
- 무한 차원 공간 : RBF 커널은 입력 데이터를 무한 차원으로 매핑하여, 복잡한 데이터 구조를 학습할 수 있게 합니다.
- 하이퍼파라미터 조정 : ( \gamma ) 값을 조정함으로써 커널의 폭을 조절할 수 있으며, 이는 모델의 복잡도에 큰 영향을 미칩니다.
가우시안 RBF 커널의 활용
가우시안 RBF 커널은 주로 다음과 같은 분야에서 활용됩니다:
- 서포트 벡터 머신(SVM): 비선형 분류 문제를 해결하는 데 매우 효과적입니다.
- 클러스터링 : 데이터 포인트 간의 유사성을 기반으로 클러스터를 형성하는 데 사용됩니다.
- 회귀 분석 : 비선형 회귀 문제를 해결하는 데 유용합니다.
가우시안 RBF 커널과 다른 커널 함수 비교
가우시안 RBF 커널은 여러 다른 커널 함수와 비교할 때 다음과 같은 차별점을 가집니다:
- 선형 커널 : 선형 커널은 데이터가 선형적으로 분포되어 있을 때 사용되며, RBF 커널보다 단순합니다.
- 다항 커널 : 다항 커널은 데이터의 다항식 관계를 모델링하는 데 사용되며, RBF 커널보다 더 복잡한 형태를 가집니다.
- 시그모이드 커널 : 시그모이드 커널은 신경망의 활성화 함수와 유사한 형태를 가지며, RBF 커널과는 다른 특성을 보입니다.

가우시안 RBF 커널의 장단점
가우시안 RBF 커널의 장점은 다음과 같습니다:
- 유연성 : 다양한 형태의 데이터에 적응할 수 있는 유연성을 제공합니다.
- 비선형성 : 비선형 문제를 효과적으로 해결할 수 있습니다.
하지만 단점도 존재합니다:
- 하이퍼파라미터 조정 필요 : ( \gamma ) 값을 적절히 조정하지 않으면 과적합이나 과소적합이 발생할 수 있습니다.
- 계산 비용 : 대규모 데이터셋에서는 계산 비용이 많이 소요될 수 있습니다.
마무리
가우시안 RBF 커널은 기계학습에서 매우 중요한 도구로, 비선형 문제를 해결하는 데 큰 도움을 줍니다. 다양한 분야에서 활용되며, 그 유연성과 강력한 성능 덕분에 많은 연구자와 개발자들이 선호하는 커널 중 하나입니다. 앞으로도 이 커널을 활용한 다양한 연구와 응용이 기대됩니다.
이 포스트가 가우시안 RBF 커널에 대한 이해를 돕는 데 도움이 되었기를 바랍니다. 추가적인 질문이 있으시면 언제든지 댓글로 남겨주세요!
태그
#가우시안RBF커널 #머신러닝 #서포트벡터머신 #비선형성 #커널함수 #데이터분석
https://link.coupang.com/a/b2FcJh
Apple 2024 맥북 프로 14 M4 - 노트북 | 쿠팡
쿠팡에서 0.0 구매하고 더 많은 혜택을 받으세요! 지금 할인중인 다른 0 제품도 바로 쿠팡에서 확인할 수 있습니다.
www.coupang.com

'Data Science' 카테고리의 다른 글
| 상관계수와 독립성 (0) | 2024.11.29 |
|---|---|
| SVM 모델과 과적합 (0) | 2024.11.29 |
| 생성형 AI와 인간의 업무 협업 관계 (4) | 2024.11.07 |
| 텍스트 분석의 단어 가방 모형 (1) | 2024.10.31 |
| 텍스트 분석의 n-gram 기법 (3) | 2024.10.31 |