https://link.coupang.com/a/b3a8pW
Apple 2024 맥북 프로 14 M4 - 노트북 | 쿠팡
쿠팡에서 0.0 구매하고 더 많은 혜택을 받으세요! 지금 할인중인 다른 0 제품도 바로 쿠팡에서 확인할 수 있습니다.
www.coupang.com
안녕하세요! 오늘은 K-means 클러스터링에서 최적의 k값을 찾는 방법에 대해 알아보겠습니다. 데이터 분석에서 클러스터링은 매우 중요한 기법이며, 그 중에서도 K-means는 가장 널리 사용되는 방법 중 하나입니다. 그럼 시작해볼까요? 😊

K-means 클러스터링 소개
K-means 클러스터링은 주어진 데이터 포인트를 k개의 클러스터로 나누는 비지도 학습 기법입니다. 이 방법은 각 클러스터의 중심(centroid)을 계산하고, 데이터 포인트를 가장 가까운 중심에 할당하여 클러스터를 형성합니다. 이 과정은 반복적으로 수행되며, 클러스터의 중심이 더 이상 변화하지 않을 때까지 진행됩니다.
K-means의 기본 개념
K-means 알고리즘은 다음과 같은 단계로 진행됩니다:
- 클러스터의 개수 k를 설정합니다.
- 데이터 포인트를 k개의 클러스터로 무작위로 초기화합니다.
- 각 데이터 포인트를 가장 가까운 클러스터 중심에 할당합니다.
- 각 클러스터의 중심을 재계산합니다.
- 3번과 4번 과정을 클러스터 중심이 더 이상 변화하지 않을 때까지 반복합니다.
이러한 과정에서 중요한 점은 최적의 k값을 선택하는 것입니다. k값이 너무 작으면 데이터가 과도하게 일반화되고, 너무 크면 클러스터가 세분화되어 의미가 없어질 수 있습니다.
최적의 k값 찾기
최적의 k값을 찾기 위해 주로 사용되는 두 가지 기법이 있습니다: 엘보우 기법과 실루엣 기법입니다.
엘보우 기법
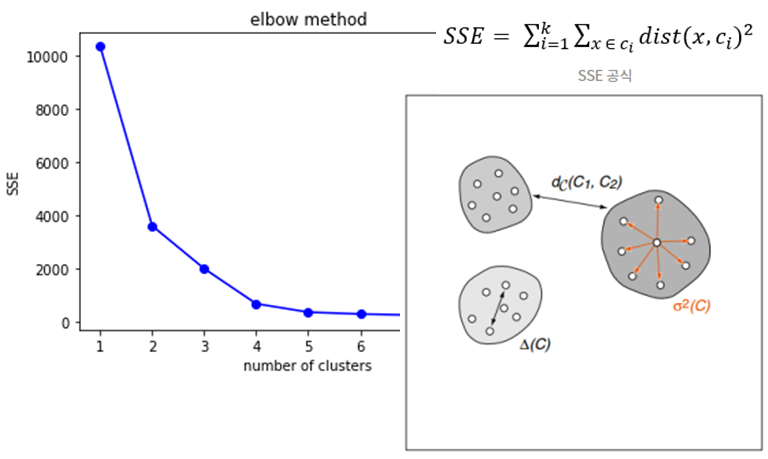
엘보우 기법은 클러스터의 개수에 따른 SSE(Sum of Squared Errors)를 시각화하여 최적의 k값을 찾는 방법입니다. SSE는 클러스터 내의 데이터 포인트와 클러스터 중심 간의 거리의 제곱합으로, 클러스터의 개수가 증가함에 따라 SSE는 감소합니다. 이때 SSE가 급격히 감소하다가 완만해지는 지점을 '엘보우 포인트'라고 하며, 이 지점이 최적의 k값으로 간주됩니다.
실루엣 기법
실루엣 기법은 각 데이터 포인트가 얼마나 잘 클러스터에 속하는지를 측정하는 방법입니다. 실루엣 계수는 -1에서 1 사이의 값을 가지며, 1에 가까울수록 해당 데이터 포인트가 잘 클러스터에 속해 있다는 것을 의미합니다. 여러 개의 k값에 대해 실루엣 계수를 계산하고, 가장 높은 값을 가지는 k값을 선택합니다.

엘보우 기법의 시각적 이해
엘보우 기법을 시각적으로 이해하기 위해, 클러스터의 개수와 SSE의 관계를 나타낸 그래프를 살펴보겠습니다. x축은 클러스터의 개수, y축은 SSE 값을 나타내며, 그래프에서 엘보우 포인트를 찾는 것이 중요합니다.

실루엣 기법의 시각적 이해
실루엣 기법의 경우, 각 클러스터에 대한 실루엣 계수를 나타내는 그래프를 통해 최적의 k값을 찾을 수 있습니다. 이 그래프에서 실루엣 계수가 가장 높은 k값을 선택하는 것이 좋습니다.

K값 선택 시 고려사항
K값을 선택할 때는 데이터의 특성과 분석 목적을 고려해야 합니다. 데이터의 분포가 불균형하거나 클러스터의 형태가 복잡한 경우, k값을 조정하여 최적의 결과를 얻는 것이 중요합니다. 또한, 여러 기법을 함께 사용하여 k값을 결정하는 것이 좋습니다.
결론 및 요약
K-means 클러스터링에서 최적의 k값을 찾는 것은 데이터 분석의 중요한 단계입니다. 엘보우 기법과 실루엣 기법을 통해 최적의 k값을 시각적으로 확인하고, 데이터의 특성을 고려하여 적절한 k값을 선택하는 것이 필요합니다. 데이터 분석을 통해 더 나은 인사이트를 얻을 수 있기를 바랍니다! 😊
태그: #Kmeans #클러스터링 #엘보우기법 #실루엣기법 #데이터분석 #기계학습 #최적k값
'Data Science' 카테고리의 다른 글
| 머신러닝에서의 데이터 전처리: 표준화, 정규화, RobustScaler (0) | 2024.12.10 |
|---|---|
| PCA에서 변수 선택과 변수 추출 차이점 (0) | 2024.12.03 |
| 상관계수와 독립성 (0) | 2024.11.29 |
| SVM 모델과 과적합 (0) | 2024.11.29 |
| 가우시안 RBF 커널의 정의 (0) | 2024.11.29 |